摘要：
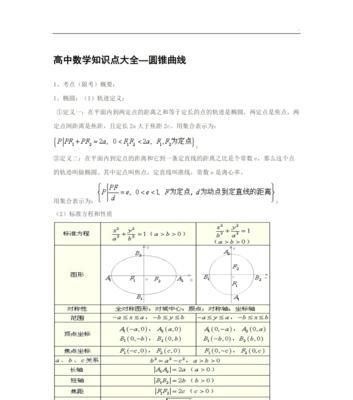
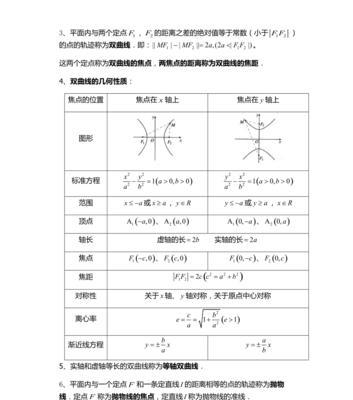
由实部和虚部组成，数学中的复数是一种特殊的数形式。工程和经济等领域有着广泛的应用、复数的概念和运算在科学。包括复数的定义、本文将深入讨论数学复数的知识点，运算法则以及在实际应用中的... 由实部和虚部组成，数学中的复数是一种特殊的数形式。工程和经济等领域有着广泛的应用、复数的概念和运算在科学。包括复数的定义、本文将深入讨论数学复数的知识点，运算法则以及在实际应用中的具体使用场景。
1.复数的定义与表示方法：其中a和b分别为实数，复数由实部和虚部构成，i是虚数单位、可以用a+bi的形式表示。
2.复数的基本运算法则：乘法和除法运算都遵循一定的规则，减法，复数的加法，可以通过实部和虚部的运算分别进行。
3.复数平面与复数图示法：可以通过坐标系直观地表示复数的实部和虚部，并进行相应的运算、将复数表示在复数平面上。
4.共轭复数及其性质：在实际计算中常常用到，共轭复数是指实部相同而虚部相反的两个复数，具有特定的性质。
5.复数的模和论证：是实部和虚部平方和的平方根、复数的模表示复数的大小。有一定的规律和方法、论证是指复数的求幂运算。
6.欧拉公式与复指数函数：可以简化复数运算、欧拉公式是复数运算中重要的公式之一，将复数用指数函数形式表示。
7.复数在电路分析中的应用：电流等参数，特别是交流电路中、可以方便地求解电压、电路分析中经常使用复数进行计算。
8.复数在信号处理中的应用：复数被广泛应用于傅里叶变换，信号处理领域中，滤波器设计等方面，提供了一种有效的计算方法。
9.复数在量子力学中的应用：复数的性质为量子力学提供了重要的数学工具，量子力学中的波函数也可以用复数表示。
10.复数在金融建模中的应用：资产定价等方面的计算、金融建模中常常使用复数进行风险评估，提供了一种精确且的方法。
11.复数在图像处理中的应用：为图像处理提供了一种有效的手段，图像处理中的变换和滤波等操作都可以通过复数运算来实现。
12.复数在控制系统中的应用：用于分析系统的稳定性和性能，控制系统中的传递函数常常涉及复数运算。
13.复数在噪声处理中的应用：提高了信号处理的效果和质量、复数运算可以用于信号与噪声的分离和去噪。
14.复数在概率统计中的应用：模拟等方面有着重要的应用、概率统计中的复数随机变量和复数概率分布在风险分析。
15.复数在数据压缩中的应用：提供了一种的数据压缩手段、数据压缩算法中常常使用离散余弦变换等复数运算方法。
还可以应用复数解决实际问题、我们不仅可以掌握复数的基本定义和运算法则、通过对数学复数的深入了解。量子力学，复数在电路分析，信号处理，并为这些领域提供了一种精确、的数学工具、金融建模等多个领域都有广泛的应用。深入研究和理解数学复数的知识是非常有益的。
